1.3 机器学习常用的包

1.3.1 NumPy

NumPy（Numerical Python）是一个开源的 Python 科学计算库，用于快速处理任意维度的数组。

NumPy 支持常见的数组和矩阵操作。

对于同样的数值计算任务，使用 NumPy 比直接使用 Python 要简洁的多。

NumPy 使用 ndarray 对象来处理多维数组，该对象是一个快速而灵活的大数据容器。

ndarray 介绍

NumPy 提供了一个N 维数组类型 ndarray，它描述了相同类型的 items 的集合。

语文	数学	英语	政治	体育
80	89	86	67	79
78	97	89	76	81

用 ndarray 进行存储：

import numpy as np

# 创建ndarray
score = np.array([[80, 89, 86, 67, 79],[78, 97, 89, 67, 81]])

# 打印结果
score

ndarray 的属性

数组属性反映了数组本身固有的信息。

属性名字	属性解释
ndarray.shape	数组维度的元组
ndarray.ndim	数组维数
ndarray.size	数组中的元素数量
ndarray.dtype	数组元素的类型

• shape：数组形状

import numpy as np

# 创建不同形状的数组
a = np.array([[1, 2, 3],[4, 5, 6]])
b = np.array([1, 2, 3, 4])
c = np.array([[[1, 2, 3],[4, 5, 6]],[[1, 2, 3],[4, 5, 6.0]]])

# 分别打印出形状
print(a.shape)
print(b.shape)
print(c.shape)

• ndim:数组维数

import numpy as np

# 创建不同形状的数组
a = np.array([[1, 2, 3],[4, 5, 6]])
b = np.array([1, 2, 3, 4])
c = np.array([[[1, 2, 3],[4, 5, 6]],[[1, 2, 3],[4, 5, 6.0]]])

# 分别打印出维数
print(a.ndim)
print(b.ndim)
print(c.ndim)

• size：数组元素数量

import numpy as np

# 创建不同形状的数组
a = np.array([[1, 2, 3],[4, 5, 6]])
b = np.array([1, 2, 3, 4])
c = np.array([[[1, 2, 3],[4, 5, 6]],[[1, 2, 3],[4, 5, 6.0]]])

# 分别打印出数组元素数量
print(a.size)
print(b.size)
print(c.size)

• dtype：数组元素的类型

import numpy as np

# 创建不同形状的数组
a = np.array([[1, 2, 3],[4, 5, 6]])
b = np.array([1, 2, 3, 4])
c = np.array([[[1, 2, 3],[4, 5, 6]],[[1, 2, 3],[4, 5, 6.0]]])

# 分别打印出数组元素数量
print(a.dtype)
print(b.dtype)
print(c.dtype)

ndarray 的类型

名称	描述
np.bool	用一个字节存储的布尔类型（True或False）
np.int8	一个字节大小，-128 至 127
np.int16	整数，-32768 至 32767
np.int32	整数，$-2^{31}$ 至 $2^{32} -1$
np.int64	整数，$-2^{63}$ 至 $2^{63} - 1$
np.uint8	无符号整数，0 至 255
np.uint16	无符号整数，0 至 65535
np.uint32	无符号整数，0 至 $2^{32} - 1$
np.uint64	无符号整数，0 至 $2^{64} - 1$
np.float16	半精度浮点数：16位，正负号1位，指数5位，精度10位
np.float32	单精度浮点数：32位，正负号1位，指数8位，精度23位
np.float64	双精度浮点数：64位，正负号1位，指数11位，精度52位
np.complex64	复数，分别用两个32位浮点数表示实部和虚部
np.complex128	复数，分别用两个64位浮点数表示实部和虚部
np.object_	python对象
np.string_	字符串
np.unicode_	unicode类型

注意：创建数组的时候指定类型

import numpy as np

# 创建数组时指定类型为 np.float32
a = np.array([[1, 2, 3],[4, 5, 6]], dtype=np.float32)

# 创建数组时未指定类型
b = np.array([[1, 2, 3],[4, 5, 6]])

# 打印结果
print("数组a：\n%s,\n数据类型：%s"%(a,a.dtype))
print("数组b：\n%s,\n数据类型：%s"%(b,b.dtype))

基本操作

生成元素值为 0 和 1 的数组的方法

• 生成全部元素值为 0 的数组

import numpy as np

zero = np.zeros([3, 4])
zero

• 生成全部元素值为 1 的数组

one = np.ones([3, 4])
one

• 生成对角数组(对角线的地方是 1，其余地方是 0)

eyes = np.eye(10, 5)
eyes

• 创建方阵对角矩阵

# np.eye(5, 5) 可简写为 (5)
eyes1 = np.eye(5)
eyes1

从现有数组生成

a = [[1, 2, 3], [4, 5, 6]]

# 从现有的数组中创建
a1 = np.array(a)
a

a1

生成固定范围的数组

# 生成等间隔的数组
a = np.linspace(0, 90, 10)
a

# 生成等间隔的数组
b = np.arange(0, 90, 10)
b

形状修改

from numpy import array
a = array([[ 0, 1, 2, 3, 4, 5],
           [10,11,12,13,14,15],
           [20,21,22,23,24,25],
           [30,31,32,33,34,35]])
a.shape

# 在转换形状的时候，一定要注意数组的元素匹配
# 只是将形状进行了修改，但并没有将行列进行转换
b = a.reshape([3, 8])
b

# 数组的形状被修改为: (2, 12), -1: 表示同过自动计算得到此处的值
c = a.reshape([-1, 12])
c

d = a.T
d.shape

类型修改

arr = np.array([[[1, 2, 3], [4, 5, 6]], [[12, 3, 34], [5, 6, 7]]])
arr.dtype

arr.astype(np.float32)

数组去重

arr = np.array([[1, 2, 3, 4],[3, 4, 5, 6]])
np.unique(arr)

数组运算

数组的算术运算是元素级别的操作，新的数组被创建并且被结果填充。

运算	函数
a + b	add(a,b)
a - b	subtract(a,b)
a * b	multiply(a,b)
a / b	divide(a,b)
a ** b	power(a,b)
a % b	remainder(a,b)

以乘法为例，数组与标量相乘，相当于数组的每个元素乘以这个标量：

import numpy as np
a = np.array([1, 2, 3, 4])
a * 3

数组按元素相乘：

a = np.array([1, 2])
b = np.array([3, 4])
a * b

使用函数

np.multiply(a, b)

函数还可以接受第三个参数，表示将结果存入第三个参数中：

np.multiply(a, b, a)

a

矩阵

使用 mat 方法将 2 维数组转化为矩阵：

import numpy as np
a = np.array([[1, 2, 4],
              [2, 5, 3],
              [7, 8, 9]])
A = np.mat(a)
A

# 也可以使用 **Matlab** 的语法传入一个字符串来生成矩阵：
A = np.mat('1,2,4;2,5,3;7,8,9')
A

矩阵与向量的乘法：

x = np.array([[1], [2], [3]])
x

A*x

b = np.array([[1, 2],
              [3, 4],
             [5, 6]])
B = np.mat(b)
A*B

A.I 表示 A 矩阵的逆矩阵：

A.I

矩阵指数表示矩阵连乘：

A ** 4

统计函数

方法	作用
a.sum(axis=None)	求和
a.prod(axis=None)	求积
a.min(axis=None)	最小值
a.max(axis=None)	最大值
a.argmin(axis=None)	最小值索引
a.argmax(axis=None)	最大值索引
a.ptp(axis=None)	最大值减最小值
a.mean(axis=None)	平均值
a.std(axis=None)	标准差
a.var(axis=None)	方差

from numpy import array
a = array([[1, 2, 3],
           [4, 5, 6]])
a

求所有元素的和：

sum(a)

a.sum()

指定求和的维度： 沿着第一维求和

np.sum(a, axis=0)

a.sum(axis=0)

沿着第二维求和：

np.sum(a, axis=1)

a.sum(axis=1)

沿着最后一维求和：

np.sum(a, axis=-1)

a.sum(axis=-1)

比较和逻辑函数

运算符	函数
==	equal
!=	not_equal
>	greater
>=	greater_equal
<	less
<=	less_equal

数组元素的比对，我们可以直接使用运算符进行比较，比如判断数组中元素是否大于某个数：

from numpy import array
a = array([[ 0, 1, 2, 3, 4, 5],
           [10,11,12,13,14,15],
           [20,21,22,23,24,25],
           [30,31,32,33,34,35]])

a > 10

# 判断数组中元素大于10的元素赋值为 -10 
a[a > 10] = -10
a

但是当数组元素较多时，查看输出结果便变得很麻烦，这时我们可以使用all()方法，直接比对矩阵的所有对应的元素是否满足条件。假如判断某个区间的值是否全是大于 20:

from numpy import array
a = array([[ 0, 1, 2, 3, 4, 5],
           [10,11,12,13,14,15],
           [20,21,22,23,24,25],
           [30,31,32,33,34,35]])

a[1:3,1:3]

np.all(a[1:3,1:3] > 20)

使用 any() 来判断数组某个区间的元素是否存在大于 20的元素:

np.any(a[1:3,1:3] > 20)

IO 操作

savetxt 可以将数组写入文件，默认使用科学计数法的形式保存：

import numpy as np

data = np.array([[1, 2],
                 [3, 4]])

# 保存文件
np.savetxt('out.txt', data)

# 读取文件
with open('out.txt') as f:
    for line in f:
        print(line)

# 读取文件
np.loadtxt('out.txt')

1.3.2 Pandas

• Pandas 是基于 NumPy 的一种工具,该工具是为了解决数据分析任务而创建的
• Pandas 纳入了大量库及一些标准的数据模型，提供了高效的操作大型数据集所需要的工具
• Pandas 提供了大量能使我们快速便捷地处理数据的函数与方法
• 是 Python 成为强大而高效的数据分析环境的重要因素之一

import pandas as pd
import numpy as np

产生 Pandas 对象

pandas 主要有两种基本的数据结构：

• Series
  • Series 是带索引的一维数组，可存储整数、浮点数、字符串、Python 对象等类型的数据。
• DataFrame
  • DataFrame 是由多种类型的列构成的二维标签数据结构，类似于 Excel 、SQL 表，或 Series 对象构成的字典。DataFrame 是最常用的 Pandas 对象。

# 生成 series
s = pd.Series([1,3,5,np.nan,6,8])
print(s)

# 生成 dataframe 
dates = pd.date_range('20200101', periods=15)
df = pd.DataFrame(np.random.randn(15,4), index=dates, columns=list('ABCD'))
df

默认情况下，如果不指定 index 参数和 columns，那么他们的值将用从 0 开始的数字替代。

写入 csv 文件：

df.to_csv('foo.csv')

读取 csv 文件：

df1 = pd.read_csv('foo.csv',index_col=0)
df1.head()

head 和 tail 方法可以分别查看最前面几行和最后面几行的数据（默认为 5）：

df1.tail(10)

了解更多Pandas内容，可以参考：https://pandas.pydata.org/pandas-docs/stable/getting_started/index.html

1.3.3 Matplotlib

简单来说，Matplotlib 是 Python 的一个绘图库。它包含了大量的工具，你可以使用这些工具创建各种图形，包括简单的散点图，正弦曲线，甚至是三维图形。

Python 科学计算社区经常使用它完成数据可视化的工作。

%matplotlib inline

import matplotlib.pyplot as plt
import numpy as np

画一个简单的图形

# 简单的绘图
x = np.linspace(0, 2 * np.pi, 50)

# 如果没有第一个参数 x，图形的 x 坐标默认为数组的索引
plt.plot(x, np.sin(x)) 

# 显示图形
plt.show() 

在一张图上绘制两条曲线

x = np.linspace(0, 2 * np.pi, 50)
plt.plot(x, np.sin(x),
         x, np.cos(x))
plt.show()

自定义曲线的外观

x = np.linspace(0, 2 * np.pi, 50)
plt.plot(x, np.sin(x), 'r-^',
         x, np.cos(x), 'g--')
plt.show()

• 颜色：

  • 蓝色 - 'b'
  • 绿色 - 'g'
  • 红色 - 'r'
  • 青色 - 'c'
  • 品红 - 'm'
  • 黄色 - 'y'
  • 黑色 - 'k'（'b'代表蓝色，所以这里用黑色的最后一个字母）
  • 白色 - 'w'

• 线：

  • 直线 - '-'
  • 虚线 - '--'
  • 点线 - ':'
  • 点划线 - '-.'

• 常用点标记:

  • 点 - '.'
  • 像素 - ','
  • 圆 - 'o'
  • 方形 - 's'
  • 三角形 - '^'

可以在这里查看更多的样式

使用子图

使用子图可以在一个窗口绘制多张图。在调用 plot() 函数之前需要先调用 subplot() 函数。该函数的第一个参数代表子图的总行数，第二个参数代表子图的总列数，第三个参数代表活跃区域。

x = np.linspace(0, 2 * np.pi, 50)
plt.subplot(2, 1, 1) # （行，列，活跃区）
plt.plot(x, np.sin(x), 'r')
plt.subplot(2, 1, 2)
plt.plot(x, np.cos(x), 'g')
plt.show()

散点图

散点图是一堆离散点的集合。用 Matplotlib 画散点图也同样非常简单。只需要调用 scatter() 函数并传入两个分别代表 x 坐标和 y 坐标的数组即可。

# 简单的散点图
x = np.linspace(0, 2 * np.pi, 50)
y = np.sin(x)
plt.scatter(x,y)
plt.show()

调整点的大小和颜色

可以给每个点赋予不同的大小

x = np.random.rand(100)
y = np.random.rand(100)
size = np.random.rand(100) * 50
plt.scatter(x, y, size)
plt.show()

也可以给每个点赋予不同颜色。

x = np.random.rand(100)
y = np.random.rand(100)
size = np.random.rand(100) * 50
color = np.random.rand(100)
plt.scatter(x, y, size, color)
plt.colorbar()
plt.show()

直方图

使用 hist() 函数可以非常方便的创建直方图。第二个参数代表分段的个数。分段越多，图形上的数据条就越多。

x = np.random.randn(1000)
plt.hist(x, 50)
plt.show()

标题，标签和图例

当需要快速创建图形时，你可能不需要为图形添加标签。但是当构建需要展示的图形时，你就需要添加标题，标签和图例。

x = np.linspace(0, 2 * np.pi, 50)
plt.plot(x, np.sin(x), 'r-x', label='Sin(x)')
plt.plot(x, np.cos(x), 'g-^', label='Cos(x)')

# 展示图例
plt.legend()

# 给 x 轴添加标签
plt.xlabel('Rads')

# 给 y 轴添加标签
plt.ylabel('Amplitude')

# 添加图形标题
plt.title('Sin and Cos Waves')

plt.show()

图片保存

fruits = ['apple', 'orange', 'pear']
sales = [100,250,300]
plt.pie(sales, labels=fruits)
plt.savefig('pie.png')
plt.show()

可以在这里查看更多的图例。

Seaborn

Seaborn 基于 matplotlib， 可以快速的绘制一些统计图表。

import seaborn as sns
import pandas as pd
sns.set()
iris = pd.read_csv("iris.csv")
sns.jointplot(x="sepal_length", y="petal_length", data=iris)

sns.pairplot(data=iris, hue="species")

可以在这里查看更多的示例。

1.3.4 Scikit-learn

• Python 语言的机器学习工具
• Scikit-learn 包括大量常用的机器学习算法
• Scikit-learn 文档完善，容易上手

机器学习算法

机器学习算法是一类从数据中自动分析获得规律，并利用规律对未知数据进行预测的算法。

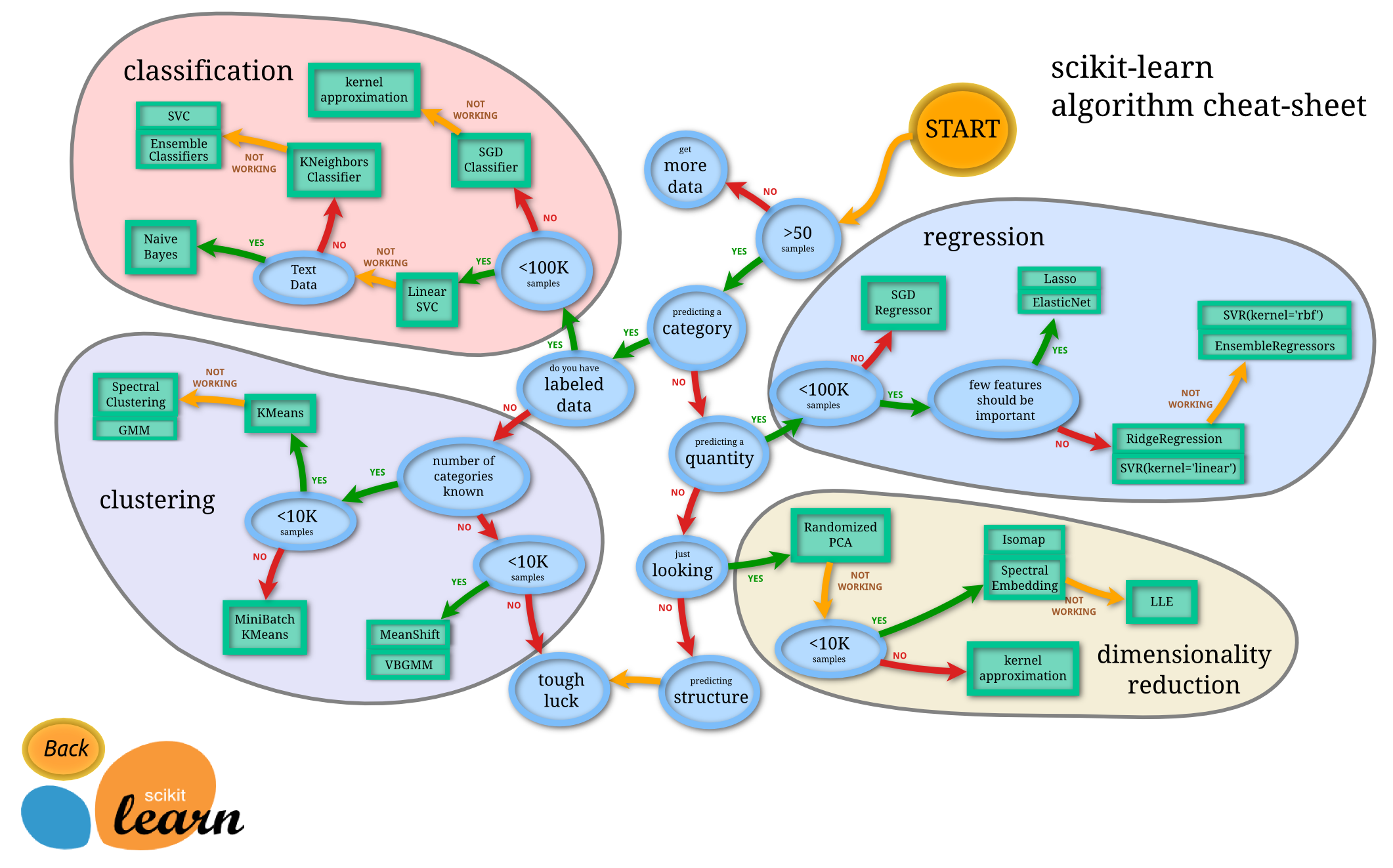
由图中，可以看到机器学习 sklearn 库的算法主要有四类：分类，回归，聚类，降维。其中：

• 常用的回归：线性、决策树、SVM、KNN ；
  集成回归：随机森林、Adaboost、GradientBoosting、Bagging、ExtraTrees
• 常用的分类：线性、决策树、SVM、KNN、朴素贝叶斯；
  集成分类：随机森林、Adaboost、GradientBoosting、Bagging、ExtraTrees
• 常用聚类：k 均值（K-means）、层次聚类（Hierarchical clustering）、DBSCAN
• 常用降维：LinearDiscriminantAnalysis、PCA 　　

这个流程图代表：蓝色圆圈是判断条件，绿色方框是可以选择的算法，我们可以根据自己的数据特征和任务目标去找一条自己的操作路线。

sklearn 数据集

• sklearn.datasets.load_*()
  • 获取小规模数据集，数据包含在 datasets 里
• sklearn.datasets.fetch_*(data_home=None)
  • 获取大规模数据集，需要从网络上下载，函数的第一个参数是 data_home，表示数据集下载的目录,默认是 /scikit_learn_data/

sklearn 常见的数据集如下：

	数据集名称	调用方式	适用算法	数据规模
小数据集	波士顿房价	load_boston()	回归	506*13
小数据集	鸢尾花数据集	load_iris()	分类	150*4
小数据集	糖尿病数据集	load_diabetes()	回归	442*10
大数据集	手写数字数据集	load_digits()	分类	5620*64
大数据集	Olivetti脸部图像数据集	fetch_olivetti_facecs	降维	400*64*64
大数据集	新闻分类数据集	fetch_20newsgroups()	分类	-
大数据集	带标签的人脸数据集	fetch_lfw_people()	分类、降维	-
大数据集	路透社新闻语料数据集	fetch_rcv1()	分类	804414*47236

from sklearn.datasets import load_iris
# 获取鸢尾花数据集
iris = load_iris()
print("鸢尾花数据集的返回值：\n", iris.keys())

数据预处理

通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程。常见的有数据标准化、数据二值化、标签编码、独热编码等。

# 导入内建数据集
from sklearn.datasets import load_iris

# 获取鸢尾花数据集
iris = load_iris()

# 获得 ndarray 格式的变量 X 和标签 y
X = iris.data
y = iris.target

# 获得数据维度
n_samples, n_features = iris.data.shape

print(n_samples, n_features)

数据标准化

数据标准化和归一化是将数据映射到一个小的浮点数范围内，以便模型能快速收敛。

标准化有多种方式，常用的一种是min-max标准化（对象名为MinMaxScaler），该方法使数据落到[0,1]区间：

$x^{'}=\frac{x-x_{min}}{x_{max} - x_{min}}$

# min-max标准化
from sklearn.preprocessing import MinMaxScaler

sc = MinMaxScaler()
sc.fit(X)
results = sc.transform(X)
print("放缩前：", X[1])
print("放缩后：", results[1])

另一种是Z-score标准化（对象名为StandardScaler），该方法使数据满足标准正态分布：

$x^{'}=\frac{x-\overline {X}}{S}$

# Z-score标准化
from sklearn.preprocessing import StandardScaler

#将fit和transform组合执行
results = StandardScaler().fit_transform(X) 

print("放缩前：", X[1])
print("放缩后：", results[1])

归一化（对象名为Normalizer，默认为L2归一化）：

$x^{'}=\frac{x}{\sqrt{\sum_{j}^{m}x_{j}^2}}$

# 归一化
from sklearn.preprocessing import Normalizer

results = Normalizer().fit_transform(X)

print("放缩前：", X[1])
print("放缩后：", results[1])

数据二值化

使用阈值过滤器将数据转化为布尔值，即为二值化。使用Binarizer对象实现数据的二值化：

# 二值化，阈值设置为3
from sklearn.preprocessing import Binarizer

results = Binarizer(threshold=3).fit_transform(X)

print("处理前：", X[1])
print("处理后：", results[1])

标签编码

使用 LabelEncoder 将不连续的数值或文本变量转化为有序的数值型变量：

# 标签编码
from sklearn.preprocessing import LabelEncoder
LabelEncoder().fit_transform(['apple', 'pear', 'orange', 'banana'])

独热编码

对于无序的离散型特征，其数值大小并没有意义，需要对其进行one-hot编码，将其特征的m个可能值转化为m个二值化特征。可以利用OneHotEncoder对象实现：

# 独热编码
from sklearn.preprocessing import OneHotEncoder

results = OneHotEncoder().fit_transform(y.reshape(-1,1)).toarray()

print("处理前：", X[1])
print("处理后：", results[1])

数据集的划分

机器学习一般的数据集会划分为两个部分：

• 训练数据：用于训练，构建模型
• 测试数据：在模型检验时使用，用于评估模型是否有效

划分比例：

• 训练集：70% 80% 75%
• 测试集：30% 20% 25%

sklearn.model_selection.train_test_split(x, y, test_size, random_state )

• x：数据集的特征值
• y： 数据集的标签值
• test_size： 如果是浮点数，表示测试集样本占比；如果是整数，表示测试集样本的数量。
• random_state： 随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
• return 训练集的特征值 x_train 测试集的特征值 x_test 训练集的目标值 y_train 测试集的目标值 y_test。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 加载数据集
iris = load_iris()

# 对数据集进行分割
# 训练集的特征值x_train 测试集的特征值x_test 训练集的目标值y_train 测试集的目标值y_test
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target,test_size=0.3, random_state=22)

print("x_train:", X_train.shape)
print("y_train:", y_train.shape)
print("x_test:", X_test.shape)
print("y_test:", y_test.shape)

定义模型

估计器（Estimator）

估计器，很多时候可以直接理解成分类器，主要包含两个函数：

• fit()：训练算法，设置内部参数。接收训练集和类别两个参数。
• predict()：预测测试集类别，参数为测试集。

大多数 scikit-learn 估计器接收和输出的数据格式均为 NumPy数组或类似格式。

转换器（Transformer）

转换器用于数据预处理和数据转换，主要是三个方法：

• fit()：训练算法，设置内部参数。
• transform()：数据转换。
• fit_transform()：合并 fit 和 transform 两个方法。

在 scikit-learn 中，所有模型都有同样的接口供调用。监督学习模型都具有以下的方法：

• fit：对数据进行拟合。
• set_params：设定模型参数。
• get_params：返回模型参数。
• predict：在指定的数据集上预测。
• score：返回预测器的得分。

鸢尾花数据集是一个分类任务，故以决策树模型为例，采用默认参数拟合模型，并对验证集预测。

# 决策树分类器
from sklearn.tree import DecisionTreeClassifier

# 定义模型
model = DecisionTreeClassifier()

# 训练模型
model.fit(X_train, y_train)

# 在测试集上预测
model.predict(X_test)

# 测试集上的得分（默认为准确率）
model.score(X_test, y_test)

scikit-learn 中所有模型的调用方式都类似。

模型评估

评估模型的常用方法为 K 折交叉验证，它将数据集划分为 K 个大小相近的子集（K 通常取 10），每次选择其中(K-1)个子集的并集做为训练集，余下的做为测试集，总共得到 K 组训练集&测试集，最终返回这 K 次测试结果的得分，取其均值可作为选定最终模型的指标。

# 交叉验证
from sklearn.model_selection import cross_val_score
cross_val_score(model, X, y, scoring=None, cv=10)

注意：由于之前采用了 train_test_split 分割数据集，它默认对数据进行了洗牌，所以这里可以直接使用 cv=10 来进行 10 折交叉验证（cross_val_score 不会对数据进行洗牌）。如果之前未对数据进行洗牌，则要搭配使用 KFold 模块：

from sklearn.model_selection import KFold
n_folds = 10
kf = KFold(n_folds, shuffle=True).get_n_splits(X)
cross_val_score(model, X, y, scoring=None, cv = kf)

保存与加载模型

在训练模型后可将模型保存，以免下次重复训练。保存与加载模型使用 sklearn 的 joblib：

from sklearn.externals import joblib

# 保存模型
joblib.dump(model,'myModel.pkl')

# 加载模型
model=joblib.load('myModel.pkl')
print(model)

下面我们用一个小例子来展示如何使用 sklearn 工具包快速完成一个机器学习项目。

采用逻辑回归模型实现鸢尾花分类

线性回归

在介绍逻辑回归之前先介绍一下线性回归，线性回归的主要思想是通过历史数据拟合出一条直线，因变量与自变量是线性关系，对新的数据用这条直线进行预测。 线性回归的公式如下：

$y = w_{0}+w_{1}x_{1}+...+w_{n}x_{n}=w^{T}x+b$

逻辑回归

逻辑回归是一种广义的线性回归分析模型，是一种预测分析。虽然它名字里带回归，但实际上是一种分类学习方法。它不是仅预测出“类别”， 而是可以得到近似概率预测，这对于许多需要利用概率辅助决策的任务很有用。普遍应用于预测一个实例是否属于一个特定类别的概率，比如一封 email 是垃圾邮件的概率是多少。 因变量可以是二分类的，也可以是多分类的。因为结果是概率的，除了分类外还可以做 ranking model。逻辑的应用场景很多，如点击率预测（CTR）、天气预测、一些电商的购物搭配推荐、一些电商的搜索排序基线等。

sigmoid 函数

Sigmoid 函数，呈现S型曲线，它将值转化为一个接近 0 或 1 的 y 值。
$y = g(z)=\frac{1}{1+e^{-z}}$ 其中:$z = w^{T}x+b$

鸢尾花数据集

sklearn.datasets.load_iris():加载并返回鸢尾花数据集

Iris 鸢尾花卉数据集,是常用的分类实验数据集，由 R.A. Fisher 于 1936 年收集整理的。其中包含 3 种植物种类，分别是山鸢尾（setosa）变色鸢尾（versicolor）和维吉尼亚鸢尾（virginica），每类 50 个样本，共 150 个样本。

变量名	变量解释	数据类型
sepal_length	花萼长度（单位cm)	numeric
sepal_width	花萼宽度（单位cm）	numeric
petal_length	花瓣长度（单位cm）	numeric
petal_width	花瓣宽度（单位cm）	numeric
species	种类	categorical

1.获取数据集及其信息

from sklearn.datasets import load_iris
# 获取鸢尾花数据集
iris = load_iris()
print("鸢尾花数据集的返回值：\n", iris.keys())

print("鸢尾花的特征值:\n", iris["data"][1])
print("鸢尾花的目标值：\n", iris.target)
print("鸢尾花特征的名字：\n", iris.feature_names)
print("鸢尾花目标值的名字：\n", iris.target_names)

# 取出特征值
X = iris.data
y = iris.target

2.数据划分

from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, y, test_size=0.1, random_state=0)

3.数据标准化

from sklearn.preprocessing import StandardScaler
transfer  = StandardScaler()
X_train = transfer.fit_transform(X_train)
X_test = transfer.transform(X_test)

4.模型构建

from sklearn.linear_model import LogisticRegression

estimator  = LogisticRegression(penalty='l2',solver='newton-cg',multi_class='multinomial')
estimator.fit(X_train,Y_train)

5.模型评估

print("\n得出来的权重：", estimator.coef_)
print("\nLogistic Regression模型训练集的准确率：%.1f%%" %(estimator.score(X_train, Y_train)*100))

6. 模型预测

from sklearn import metrics
y_predict = estimator.predict(X_test)
print("\n预测结果为:\n", y_predict)
print("\n比对真实值和预测值：\n", y_predict == Y_test)

# 预测的准确率
accuracy = metrics.accuracy_score(Y_test, y_predict)
print("\nLogistic Regression 模型测试集的正确率：%.1f%%" %(accuracy*100))

7.交叉验证

from sklearn.model_selection import cross_val_score
import numpy as np
scores = cross_val_score(estimator, X, y, scoring=None, cv=10)  #cv为迭代次数。
print("\n交叉验证的准确率:",np.round(scores,2))  # 打印输出每次迭代的度量值（准确度）
print("\n交叉验证结果的置信区间: %0.2f%%(+/- %0.2f)" % (scores.mean()*100, scores.std() * 2))  # 获取置信区间。（也就是均值和方差）