2.3 回归分析

回归分析：分析不同变量之间存在关系的研究。
回归模型：刻画不同变量之间关系的模型。

2.3.1 回归分析的基本概念

探究莫纳罗亚山地区二氧化碳与温度之间的关系

数据：下表给出了莫纳罗亚山从 1970 年到 2005 年间每 5 年的二氧化碳浓度，单位是百万分比浓度（parts per million，简称ppm）

莫纳罗亚山从 1970 年到 2005 年间每 5 年的二氧化碳浓度

**年份 $x$ **	1970	1975	1980	1985	1990	1995	2000	2005
**$CO_2$(ppm) $y$**	325.68	331.15	338.69	345.90	354.19	360.88	369.48	379.67

目标：分析时间年份和二氧化碳浓度之间的关联关系，由此预测2010年二氧化碳浓度。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.dpi'] = 150

x = np.array([1970, 1975, 1980, 1985, 1990, 1995, 2000, 2005])
y = np.array([325.68, 331.15, 338.69, 345.90, 354.19, 360.88, 369.48, 379.67])
fig = plt.figure()
plt.xlabel("Year")
plt.ylabel("Co2")
plt.scatter(x, y, c='r')
plt.show()

该地区二氧化碳浓度在逐年缓慢增加，因此我们使用简单的线性模型来刻画时间年份和二氧化碳浓度两者之间的关系，即 $二氧化碳浓度 = a × 时间 + b$。

设时间年份为 $x$，二氧化碳浓度为 $y$，即 $y = ax + b$ 。

通过上述数据来确定模型中 $a$ 和 $b$ 的值，一旦求解出 $a$ 和 $b$ 的值，输入任意的时间年份即可估算出该年份对应的二氧化碳浓度值。

2.3.2 回归分析中参数计算

最简单的线性回归是一元线性回归模型，只包含一个自变量 $x$ 和一个因变量 $y$，并且假定自变量和因变量之间存在 $y=ax+b$ 的线性关系。

求解参数 $a$ 和 $b$，需要给定若干组 $(x,y)$ 数据，然后从这些数据出发来计算参数 $a$ 和 $b$。

在一元线性回归模型中，最关键的问题是如何计算参数 $a$ 和参数 $b$ 使误差最小化。

最拟合直线 $y=ax+b$ 应该与这 8 组样本数据点距离都很近，最好的情况是这些样本数据点都在该直线上（不现实），让所有样本数据点离直线尽可能的近（被定义为预测数值和实际数值之间的差）。

预测值：通过给定参数 $a$ 和 $b$ 计算 $ax+b$ 得到的值记为 $\widetilde{y}=ax+b$

真实值：每组数据中 $(x,y)$ 中对应的 $y$ 值

残差：作为 $x$ 所对应的真实值 $y$ 和模型预测值 $\widetilde{y}$ 之间误差的绝对值；在实际中一般使用$(y-\widetilde{y})^2$作为残差。

回归分析中，对于不同的参数，最佳回归模型是最小化残差平方和的均值，即要求 N 组 $(x,y)$ 数据得到的残差平均值 $\frac{1}{N}\sum{（y-\widetilde{y}）^2}$ 最小。

因此，给定的 8组 $(x,y)$数据，可通过最小二乘法来求解使得残差最小的 $a$ 和 $b$。

8组 $(x,y)$ 样本数据点记为 $(x_1,y_1)$， $(x_2,y_2)$， ...， $(x_8,y_8)$， 时间年份变量 $x$ 的平均值 $\overline{x}=\frac{x_1+x_2+...+x_8}{8}$， 因变量 $y$ 的平均值为$\overline{y}=\frac{y_1+y_2+...+y_8}{8}$， 则：

$a=\frac{x_{1}y_{1}+x_2y_2+...+x_8y_8-8\overline{x}\overline{y}}{x_{1}^{2}+x_{2}^{2}+...+x_{8}^{2}-8\overline{x}^2}=1.5344$

$b = \overline{y}-a\overline{x}=-2698.9$

我们根据上面的公式编写如下的方法来求解 $a$ 和 $b$。

def cal_a_b(x, y):
    """
    计算 x 和 y 的线性系数
    :param x: np array 格式的自变量
    :param y: np array 格式的因变量
    :return: 系数 a 和 b
    """
    # 计算 x 和 y 的平均数
    x_avarage = np.sum(x) / len(x)
    y_avarage = np.sum(y) / len(y)

    # 两个临时变量用于后续计算参数 a 和 b
    # m 为 x1*y1 + x2*y2 + ... 
    # n 为 x1*x1 + x2*x2 + ... 
    m = np.sum(x * y)
    n = np.sum(x ** 2)

    # 计算参数 a 和 b
    a = (m - len(x) * x_avarage * y_avarage) / (
                n - len(x) * x_avarage * x_avarage)
    b = y_avarage - a * x_avarage
    return a, b

a, b = cal_a_b(x, y)
print(a, b)

综上：预测莫纳罗亚山地区二氧化碳浓度的一元线性回归模型为：$y=1.5344x-2698.9$。

我们可以据此绘制出拟合直线。

# 构造 y = ax + b 直线
x_predict = np.linspace(1965, 2010, 1000)
y_predict = a * x_predict + b

# 绘图
plt.rcParams['figure.dpi'] = 150
fig = plt.figure()
plt.xlabel("Year")
plt.ylabel("Co2")
plt.scatter(x, y, c='r')
plt.plot(x_predict, y_predict, c='b')
plt.show()

然后我们可以对该地区1970年之前和2005年之后的二氧化碳浓度进行估算。

# 例如，预测 2015 年的二氧化碳浓度
a * 2015 + b

最终的预测结果汇总如下：

**年份 $x$ **	1960	1965	1970-2005	2010	2015
**$CO_2$(ppm) $y$**	308.51	316.18	已有数据	385.23	392.90

扩展内容

1.使用 sklearn 工具包构建回归模型

我们也可以使用 sklearn 工具包来解决上面的问题。

# 导入工具包
import numpy as np
from sklearn.linear_model import LinearRegression

# 定义数据
x = np.array([1970, 1975, 1980, 1985, 1990, 1995, 2000, 2005]).reshape(-1,1)
y = np.array([325.68, 331.15, 338.69, 345.90, 354.19, 360.88, 369.48, 379.67]).reshape(-1,1)

# 构建模型
reg = LinearRegression()

# 使用数据训练模型
reg.fit(x, y)

# 打印模型参数
print(reg.coef_)
print(reg.intercept_)

2.梯度下降法

在上面的例子中，不同的参数 a 和 b 将带来不同的残差值。我们把残差值更统一的称为代价函数。

我们的目标就是选择合适的参数 a 和 b 来让这个代价函数的值最小。

梯度下降是一个用来求函数最小值的算法，我们可以使用梯度下降算法来求出代价函数$J(\theta_{0}, \theta_{1})$的最小值。

梯度下降背后的思想是：开始时我们随机选择一个参数的组合$(\theta_{0},\theta_{1},......,\theta_{n})$ ，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到抵达一个局部最小值，因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值，选择不同的初始参数组合，可能会找到不同的局部最小值。

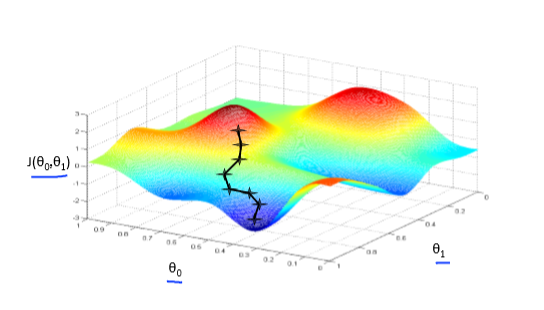
梯度下降算法的公式为：

其中 $J$ 是代价函数，$\theta_{0},\theta_{1}$ 是待求参数， $α$ 是学习率，它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。

对于线性回归，我们的代价函数的曲线是一个 U 型。

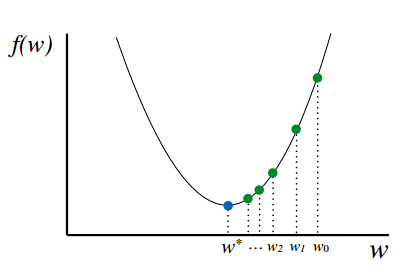
也由于代价函数曲线是 U 形，所以梯度下降算法肯定会找到其全局最小值。

梯度下降其实用途广泛，不仅可以解决回归问题，也可以用来解决分类问题。在下图可以看到模型学习的过程。

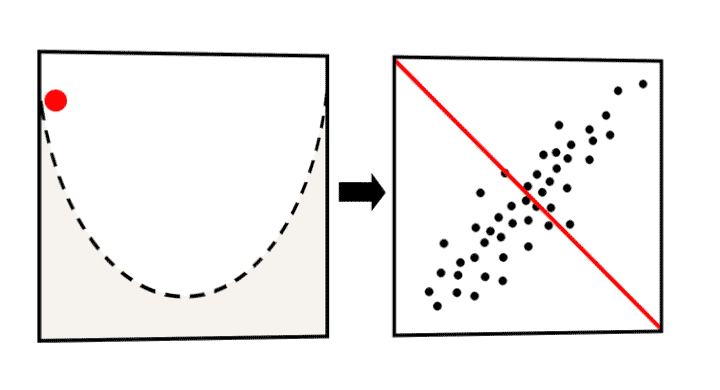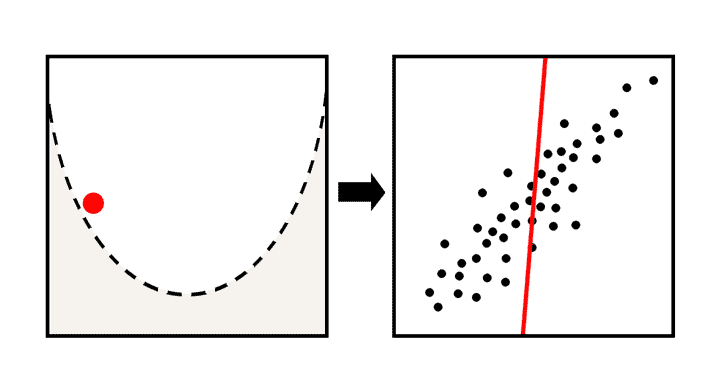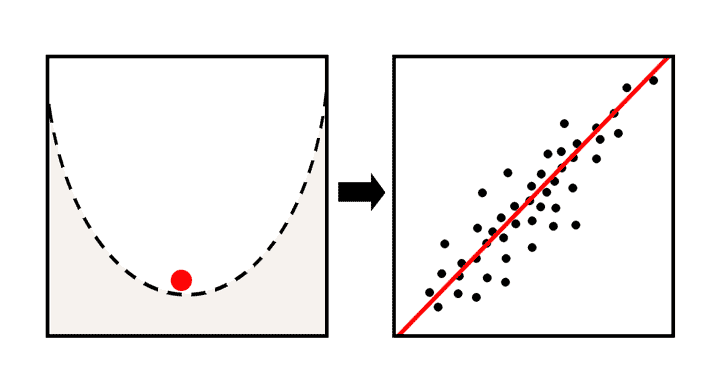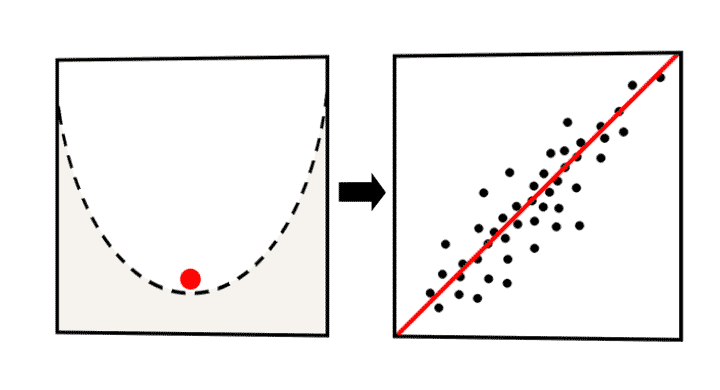
探究莫纳罗亚山地区二氧化碳与温度之间的关系

该地区 1970 年到 2005 年间每 5 年的二氧化碳浓度以及全球温度（相对于 1961 - 1990 年经过平滑处理的平均温度增长量）

$CO_2$(ppm) $x$	325.68	331.15	338.69	345.90	354.19	360.88	369.48	379.67
温度 $y$	-0.108	-0.082	0.015	0.080	0.149	0.240	0.370	0.420

我们可以使用上面同样的方法来求解得到参数 $a$ 和 $b$。并绘制出拟合直线。

# 数据
x = np.array([325.68, 331.15, 338.69, 345.90, 354.19, 360.88, 369.48, 379.67])
y = np.array([-0.108, -0.082, 0.015, 0.080, 0.149, 0.24, 0.370, 0.420])

# 计算参数 a 和 b
a, b = cal_a_b(x, y)

# 构造 y = ax + b 直线
x_predict = np.linspace(325, 380, 1000)
y_predict = a * x_predict + b

# 绘图
fig = plt.figure()
plt.xlabel("Co2")
plt.ylabel("Temperature")
plt.scatter(x, y, c='r')
plt.plot(x_predict, y_predict, c='b')
plt.show()

思考与练习

1. 摄氏温度（℃）和华氏温度（℉）是两种计量温度的标准，下表给出了两种温度之间的若干关系，如摄氏温度 0℃ 等于华氏温度 32℉。

不同温度下测得摄氏/华氏温度表

摄氏温度（℃）	0	10	15	20	25	30
华氏温度（℉）	32	50	59	68	77	86

试判断摄氏温度和华氏温度之间是否符合线性关系。如符合，请通过线性回归分析计算出摄氏温度和华氏温度之间的线性回归方程。

首先：我们观察一下摄氏华氏温度的散点图

# 数据
x = np.array([0, 10, 15, 20, 25, 30])
y = np.array([32, 50, 59, 68, 77, 86])
fig = plt.figure()
plt.xlabel("摄氏温度")
plt.ylabel("华氏温度")
plt.scatter(x, y, c='r')
plt.show()

通过散点图，我们观察到摄氏温度和华氏温度是符合线性关系的。使用我们上面写好求解参数的方法，即可快速求解。

a, b = cal_a_b(x, y)
print('参数 a 的值为：{:g}，参数 b 的值为：{:g}'.format(a, b))

# 构造 y = ax + b 直线
x_predict = np.linspace(0, 30, 1000)
y_predict = a * x_predict + b

# 绘图
fig = plt.figure()
plt.xlabel("摄氏温度")
plt.ylabel("华氏温度")
plt.scatter(x, y, c='r')
plt.plot(x_predict, y_predict, c='b')
plt.show()

1. 摩尔定律是由英特尔创始人之一的戈登·摩尔提出，其基本内容为：当价格不变时，集成电路上可容纳的元器件的数目，大约每隔 18-24 个月变会增加一倍，性能也将提升一倍。下表记录了 1971-2004 年英特尔微处理器晶体管数量的增长。需要注意的是，随着单位面积上晶体管体积越来越小，摩尔定律所描述的晶体管增长在不久的将来会面临发展的极限。

微处理器	推出年份($x$)	晶体管数量($y$)	$z$=log2$y$
4004	1971	2300	11.17
8008	1972	2500	11.29
8080	1974	4500	12.14
8086	1978	29000	14.82
Intel266	1982	134000	17.03
Intel386~processor	1985	275000	18.07
Intel486~processor	1989	1200000	20.19
Intel Pentium processor	1993	3100000	21.56
Intel Pentium Ⅱ processor	1997	7500000	22.84
Intel Pentium Ⅲ processor	1999	9500000	23.18
Intel Pentium 4 processor	2000	42000000	25.32
Intel Itanium processor	2001	25000000	24.58
Intel Itanium 2 processor	2003	220000000	27.72
Intel Itanium 2 processor(9MB cache)	2004	592000000	29.14

摩尔定律刻画了晶体管数量与时间之间存在指数关系，可用非线性回归拟合来表示这种关系，非线性回归拟合超出了本教程的内容范围。不过我们可以对晶体管数量取以 2 为底的对数（记为 $z$ ），通过判断 $z$ 与时间 $x$ 之间是否存在线性关系，来验证摩尔定律。如果上述线性关系存在，使用线性回归方法计算之间的最佳拟合直线。

# 年份
x = np.array(
    [1971, 1972, 1974, 1978, 1982, 1985, 1989, 1993, 1997, 1999, 2000, 2001,
     2003, 2004])
# 晶体管取以 2 为底的对数
z = np.array(
    [11.17, 11.29, 12.14, 14.82, 17.03, 18.07, 20.19, 21.56, 22.84, 23.18,
     25.32, 24.58, 27.72, 29.14])

我们绘图观察 $x$ 和 $z$ 之间的关系

fig = plt.figure()
plt.xlabel("年份")
plt.ylabel("晶体管取以 2 为底的对数")
plt.scatter(x, z, c='r')
plt.show()

我们看到 $z$ 与时间 $x$ 之间是否存在线性关系，我们用上面写好的方法来求解系数。

a, b = cal_a_b(x, z)
print('参数 a 的值为：{:g}，参数 b 的值为：{:g}'.format(a, b))

# 构造 y = ax + b 直线
x_predict = np.linspace(1970, 2005, 1000)
z_predict = a * x_predict + b

# 绘图
fig = plt.figure()
plt.xlabel("年份")
plt.ylabel("晶体管取以 2 为底的对数")
plt.scatter(x, z, c='r')
plt.plot(x_predict, z_predict, c='b')
plt.show()

扩展阅读

1. 线性回归白板推导
2. sklearn 线性回归